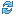Пусть у=АОМ будет некоторый острый угол, стороны которого суть OA и ОМ. Выберем на стороне ОМ произвольную точку Р и опустим перпендикуляр РХ на другую сторону OA угла у. Мы получим прямоугольный треугольник ОХР\ в нем отношение.
Эти отношения называются тригонометрическими величина ми данного угла у. Для краткости тригонометрические величины обозначаются следующим образом:
Пусть тригонометрические величины тупого угла. Пусть //= ЛОМ будет некоторый тупой угол. Выберем, как и в случае острого угла, на одной из сторон, напр., ОМ' произволь ную точку Р и опустим из нее перпендикуляр P'N' на * OA — продолжение основной стороны OA данного тупого у \ угла АОМ\ он пересечет
-п jy' продолжение OA в точке N'.
Применяя правило Декарта, мы условимся принимать отрезки, направленные от вершины д<шного угла по одной из его сторон, за положительные, а направленные в противоположную сторону, или от вершины данного угла по продолжению его стороны, за отрицательные Для тупого угла линия ON, как направленная от точки О не по стороне данного угла, а по ее продолжению, в сторону, противоположную счету положительных направлений, является отрицательною, перпендикуляр же P'2V , как пересекающий продолжение стороны данного угла, считается положительным (см конец § 3).
Распространяя определение тригонометрических величин на тупой угол, мы напишем:
отрицательного. Так как значение - избрано произвольно, ми
1ft
заключаем, что каждому из всевозможных значений тангенса может быть найден угол; а так как числа изменяются нечр( -рывно, то и тангенс обладает свойством непрерывности.


 Просмотров
Просмотров